티스토리 뷰
지난 스택(Stack)편에 이어 이번 시간에는 큐(Queue)에 대해 알아보겠다.
스택(Stack) 편 link
https://algoroot.tistory.com/54
[알고리즘, 자료구조] 자바스크립트로 스택(Stack)구현하기
어떤 데이터의 구체적인 구현 방식은 생략한 채, 데이터의 추상적 형태와 그 데이터를 다루는 방법만을 정해놓은 것을 가지고 ADT(Abstract Data Type) 혹은 추상 자료형이라고 한다. 그 중 널리 사
algoroot.tistory.com
큐 (Queue)
- First in, First out 원칙으로 만들어진 자료구조 > 먼저 들어온 데이터가 먼저 나간다.
- 자바스크립트 엔진에서 비동기 함수 실행시 콜백들이 대기열로 들어오는 Task queue가 대표적 예이다.
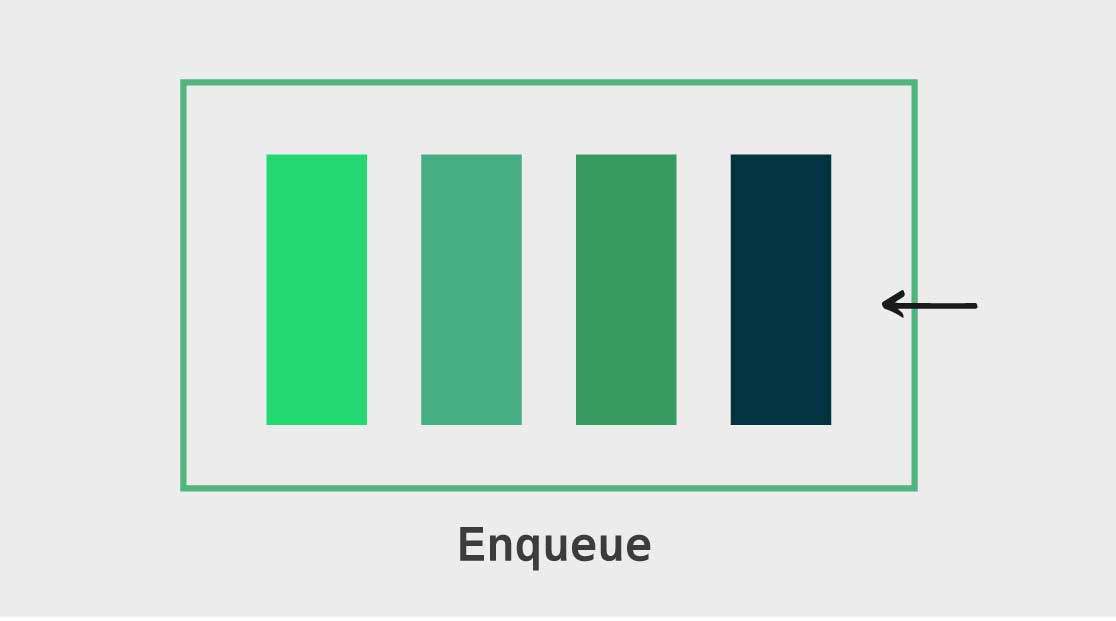
- 데이터를 집어넣는 enqueue, 데이터를 추출하는 dequeue 등의 작업을 할 수 있다.
- 큐는 순서대로 처리해야 하는 작업을 임시로 저장해두는 버퍼(buffer)로서 많이 사용된다.

속성
- first : 큐 맨 앞의 아이템
메소드
- dequeue : 큐 맨 앞의 아이템을 제거하고 및 그 아이템을 반환한다
- enqueue : 큐에 아이템을 추가한다
- contains : 해당 아이템이 큐에 존재하는지 확인한다
- size : 현재 큐에 있는 아이템의 총 개수를 반환한다
큐 (Queue) 사용 사례
데이터가 입력된 시간 순서대로 처리해야 할 필요가 있는 상황에 이용한다.
- 너비 우선 탐색(BFS, Breadth-First Search) 구현
- 처리해야 할 노드의 리스트를 저장하는 용도로 큐(Queue)를 사용한다.
- 노드를 하나 처리할 때마다 해당 노드와 인접한 노드들을 큐에 다시 저장한다.
- 노드를 접근한 순서대로 처리할 수 있다.
- 캐시(Cache) 구현
- 우선순위가 같은 작업 예약 (인쇄 대기열)
- 선입선출이 필요한 대기열 (티켓 카운터)
- 콜센터 고객 대기시간
- 프린터의 출력 처리
- 윈도 시스템의 메시지 처리기
- 프로세스 관리
JavaScript 배열로 큐(Queue) 구현
dequeue()에서 shift() 를 사용해 간단히 구현할 수 는 있다. 하지만 shift()특성상 배열 맨 앞의 요소(0번째 요소) 를 삭제하게 되면 배열의 길이(length)만큼 기존 요소들을 앞으로 당겨줘야하므로 시간복잡도가 O(n)이 되어버린다.
정석대로의 큐(Queue)라면 시간복잡도가 O(1)이 되어야한다.
export default class Queue {
constructor() {
// item들을 받을 배열 생성
this.items = [];
}
enqueue(item) {
this.items.push(item);
}
dequeue() {
return this.items.shift();
}
peek() {
return this.items[0];
}
getSize() {
return this.items.length;
}
isEmpty() {
return this.getSize() === 0;
}
}
배열을 이용하지 않고 큐(Queue) 구현 ( In JavaScript)
시간복잡도를 O(1)으로 하기 위해 연결리스트(LInked List)를 통해 큐(Queue)를 자바스크립트(JavaScript)로 구현해보겠다.
class Node {
constructor(data) {
this.data = data;
this.next = null;
}
}
class Queue {
constructor() {
this.front = null;
this.rear = null;
}
isEmpty() {
return this.front == null && this.rear === null;
}
insert(data) {
const newNode = new Node(data);
if (this.isEmpty()) this.front = newNode;
else this.rear.next = newNode;
// after doing all that we are going to shift the new node rear pointer to the new node
this.rear = newNode;
}
remove() {
if (this.isEmpty()) return;
this.front = this.front.next;
// this.front == null
// previously in the queue there was only one element and that was deleted
// so this.rear have to be shifted to newNode;
if (!this.front) this.rear = null;
}
peekFront() {
if (this.isEmpty()) return -404;
return this.front.data;
}
display() {
if (this.isEmpty()) return;
let curr = this.front;
process.stdout.write("(FRONT) ");
// when the curr hits the rear pointer is going to stop.
// it will make curr to stop at the last node.
while (curr != this.rear) {
process.stdout.write(`${curr.data} ---> `);
curr = curr.next;
}
process.stdout.write(`${this.rear.data} (REAR)\n`);
}
}

프린트 테스트까지 완료.
큐(Queue)의 Big-O (Time Complexity)
Insertion : 큐(Queue)에 데이터를 추가하는 것은 큐(Queue)의 맨 뒤 요소(rear) 에 하나를 추가(push) 하면된다. 스택에 들어있는 값들이 무수히 많아도 하나의 데이터의 삽입은 한 번이기 때문에 시간 복잡도는 O(1)이 된다.
delete : FIFO에 따라 삭제를 할 때도 첫 번째 데이터(front)가 삭제되는 것이므로 스택의 크기에 상관없이 시간복잡도는 O(1)이된다.
Access : 큐(Queue) 특성상 한쪽 끝(rear) 으로만 자료를 넣고 뺄 때는 첫 번째 데이터(front)가 빠지게 되는 자료구조이므로 데이터 접근 또한 첫 번째 데이터(front)를 통해서만 접근이 가능하다. 삭제 또한 첫 번째 데이터(front)을 통해서만 가능하다. 따라서 n번 째 접근은 첫 번째 데이터(front)부터 순회하기 때문에 O(n)의 시간복잡도를 가진다.
Search : 데이터를 찾을 때 만약 큐(Queue)의 첫 번째 데이터(front)를 찾는다면 시간복잡도는 O(1)일 것이다. 하지만 가장 뒤에있는 데이터를(rear) 찾는다면 데이터의 개수만큼 작업이 발생되므로 시간복잡도는 O(n)이 되겠다.
| Big-O (시간복잡도) | 삽입 | 삭제 | 접근 | n번째 접근 | 검색 |
| 큐 (Queue) | O(1) | O(1) | O(1) | O(n) | O(n) |
빼놓을 수 없는 스택(Stack) 자료구조 이해 & 구현하기!
https://algoroot.tistory.com/54
[알고리즘, 자료구조] 자바스크립트로 스택(Stack)구현하기
어떤 데이터의 구체적인 구현 방식은 생략한 채, 데이터의 추상적 형태와 그 데이터를 다루는 방법만을 정해놓은 것을 가지고 ADT(Abstract Data Type) 혹은 추상 자료형이라고 한다. 그 중 널리 사
algoroot.tistory.com
Reference
https://gmlwjd9405.github.io/2018/08/02/data-structure-queue.html
https://makasti.tistory.com/92
https://www.youtube.com/watch?v=LbAKOE5_Du4
https://www.youtube.com/watch?v=iY0Ab5z5jY0
'알고리즘 > 자료구조' 카테고리의 다른 글
| [알고리즘, 자료구조] 힙 Heap 자바스크립트로 구현하기 (0) | 2022.03.25 |
|---|---|
| [알고리즘, 자료구조] 자바스크립트로 해시테이블(Hash Table) 구현하기 (+개념이해) (0) | 2022.03.17 |
| [알고리즘, 자료구조] 자바스크립트로 스택(Stack)구현하기 (+개념이해) (0) | 2022.03.15 |
- Total
- Today
- Yesterday
- 리액트
- network
- 타입스크립트
- React Query
- github
- 항해99
- css
- 프로그래머스
- python
- 자바스크립트
- GIT
- 클로저
- 자바스크립트알고리즘
- 자바스크립트 비동기 처리
- 프로그래머스 자바스크립트
- 알고리즘자바스크립트
- 리액트네이티브
- 네트워크
- reactquery
- 프로그래머스 베스트앨범 자바스크립트
- javascript
- 무한스크롤
- html
- 모두를위한컴퓨터과학
- 백준
- 실전프로젝트
- React
- 모두를 위한 컴퓨터 과학
- cs50
- 자바스크립트 클로저
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
